[bibshow file=ref.bib]

Dando continuidade ao método de estimação de formantes baseado na ideia utilizada no TCC e no PIBIC, apresento nesse relatório novos testes que realizei e os resultados que obtive. Tendo em vista a melhoria do que apresentei no relatório anterior, utilizei uma abordagem um pouco mais refinada para a remoção da frequência fundamental – que vinha atrapalhando a estimação das formantes (especialmente a primeira formante).

Ué, mas você não disse que ia fazer uma pausa nos relatórios? O que foi feito dessa vez?

Bem observado de sua parte. De fato, eu havia dito. Mas acabou que as ideias começaram a coçar em minha cabeça e, bem… cheguei até aqui. De uma forma geral, mantive a estrutura do método como apresentado anteriormente, focando as alterações na remoção da influência da frequência fundamental da estimação.

Sim, aquele método! Bem… como ele era mesmo?

Não se preocupe, farei uma breve recapitulação sobre ele. A ideia inicial do método consiste em estimar as formantes utilizando os picos do contorno espectral do sinal. Porém, dependendo do sinal analisado, preditores de mesma ordem podem retornar um diferente número de picos espectrais. Assim propus a utilização de preditores lineares de diversas ordens para uma estimação mais acurada das formantes. Para isso, é escolhido o preditor de maior ordem, que encontre uma formante a mais que o número desejado em seu contorno espectral, para analisar o valor das formantes.

Os sinais sintetizados

Utilizei, para avaliar o resultado da estimação, os mesmos três sinais de voz sintetizados do relatório anterior. Esses sinais são equivalente à vogal /a/, com valores de frequência fundamental ( $f_0$ ) iguais a 110Hz, 205Hz e 300Hz. Os valores das formantes são os representados na Tabela 1, apresentados em Behlau [bibcite key=Behlau2001].

Rendered by QuickLaTeX.com

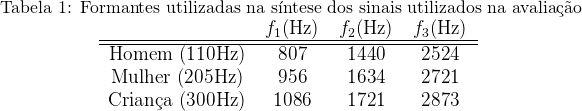
As medidas para avaliar o método

Para avaliar os valores estimados realizei o cálculo das mesmas duas medidas utilizadas no relatório anterior: o erro percentual por formante [bibcite key=wang2010high] e a distância euclidiana entre o vetor das formantes e o vetor das formantes estimadas [bibcite key=alku2013formant].

O resultado anterior

Rendered by QuickLaTeX.com

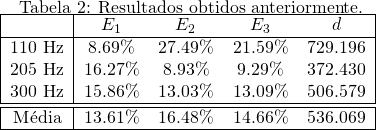
Utilizando a segunda abordagem proposta no relatório anterior (que foi significativamente melhor), em que a contagem dos picos no contorno espectral foi feita no trecho do espectro com frequências maiores que $300$ Hz (para assegurar que os picos espectrais proporcionados pela frequência fundamental não seriam considerados) foram obtidos os valores do erro percentual por formante e da distância euclidiana apresentados na Tabela 2.

Ah, lembrei! Mas e agora?

Pensando em melhorar a remoção da influência da $f_0$ do sinal, implementei um processo utilizando estimação de $f_0$ por autocorrelação do sinal, predição linear e filtragem inversa. Mas caso esteja perguntando “o que é mesmo isso?”, seus problemas se acabaram! Farei um breve introdução/revisão desses conceitos¹.

Estimação de frequência fundamental por autocorrelação

Para estimar a $f_0$ de um sinal, é necessário que a repetição periódica seja detectada. Uma maneira bem simples de fazer isso consiste em utilizar a função de autocorrelação. Assumindo um sinal digital $x[k]$ , a função de autocorrelação $\phi[k]$ desse sinal é dada pelo produto interno de um sinal com ele mesmo defasado em $k$ amostras, como mostrado na seguinte equação [bibcite key=Rabiner1978]:

(1) $\begin{equation*} \phi[k]=\sum_{m=-\infty}^{\infty} {x[m]x[m+k]}. \end{equation*}$

Aqui é possível observar que o valor máximo desse função é atingido quando $k=0$ . Porém, quando a autocorrelação é calculada com um sinal periódico, a função de autocorrelação vai ser periódica com o mesmo período do sinal, i.e., para $k=nP$ (onde $P$ é o período e $n$ é um número inteiro qualquer), $\phi[0]=\phi[k]$ . Como o sinal de voz não é exatamente algo que possamos chamar de periódico, podemos estimar o período do sinal observando o segundo maior pico do sinal de autocorrelação (o maior pico equivale a $k=0$ ). O valor de k que fornece esse pico equivale ao período (em amostras) do sinal. Assim, conhecendo o período e a taxa de amostragem do sinal, podemos estimar a $f_0$ .

Na Figura 1 ilustrei um sinal e seu respectivo sinal de auto correlação e gerei uma ilustração animada do processo de calculo do sinal de auto correlação pra um sinal, disponível no link: https://www.youtube.com/watch?v=LMbIj9B5MfI.

Filtragem Inversa

O processo de filtragem inversa nada mais do que literalmente “inverter” um filtro para anular seu efeito no sinal, “transformando” polos em zeros e vice-versa. Assim, se quisermos remover a influência exercida por um filtro $H(z)$ de um sinal que foi filtrado por ele, basta utilizar um filtro $G(z)$ , dado como segue:

(2) $\begin{equation*} G(z)={H(z)}^{-1}. \end{equation*}$

Sei que isso parece completamente nada a ver com o ponto que se deseja chegar com esse relatório, mas peço que tenha calma. Logo vai dar pra entender (eu espero).

Ok então, estou calmo. Como você usou isso tudo pra melhorar o resultado?

Bem, inicialmente pensei em estimar a $f_0$ do sinal utilizando autocorrelação e daí passar o sinal por um filtro passa-altas com frequência de corte um pouco maior que a própria $f_0$ . Porém, poupá-los-ei² de mais uma tabela e já adianto que os resultados obtidos dessa forma não foram bons. O porque desses resultados não terem sido bons, sinceramente, eu ainda não sei.

Entretanto, após ter chegado nesse resultado, pensei em uma outra forma de remover a influência da fundamental, sem remover outros componentes de frequência do sinal. Tendo estimado a $f_0$ , passei o sinal por um filtro passa-faixa de banda estreita (100Hz de banda passante) centrado na $f_0$ . Em seguida, apliquei um preditor linear de segunda ordem ao sinal filtrado e, com os coeficientes estimados pelo preditor, apliquei filtragem inversa no sinal original para remover, assim, a influência da $f_0$ . Por fim, apliquei o processo proposto no relatório anterior, para estimar formantes, no sinal resultante da filtragem inversa. Todo esse processo pode ser representado pelo diagrama de blocos ilustrado na Figura 2. A Figura 3 exemplifica o efeito da filtragem inversa, removendo o efeito da $f_0$ no contorno espectral estimado.

Figura 2 – Diagrama de blocos da abordagem proposta.

$\Rightarrow$ $=$
Figura 3 – Exemplo do efeito da filtragem inversa na estimação do contorno espectral: (a) Contorno espectral de um sinal, estimado por um preditor linear de ordem 10; (b) Contorno espectral estimado para o sinal que passou pelo filtro passa-faixa centrado na $f_0$ do sinal, representado em azul tracejado. O sinal de (a) é então passado pelo filtro inverso, cujo contorno espectral é representado pela linha laranja; (c) Contorno espectral do sinal resultante da filtragem inversa, estimado também com um preditor de ordem 10.

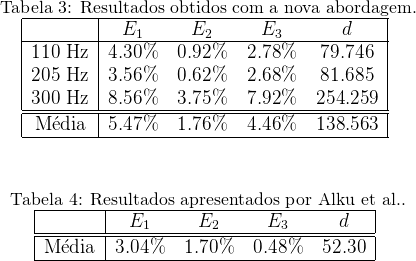
Os resultados que eu obtive utilizando essa nova proposta encontram-se representados na Tabela 3. Nela podemos observar uma melhora significativa na estimação das formantes. Assim como no relatório anterior, na Tabela 4 estão representados os resultados do trabalho de Alku et al. [bibcite key=alku2013formant] para fins de comparação.

Rendered by QuickLaTeX.com

Caramba, melhorou bastante mesmo! E agora, quais os próximos passos?

De fato, os resultados foram bem satisfatórios dessa vez. Para a continuidade do trabalho, tem dois pontos aos quais creio que seja necessário dispensar atenção a partir daqui:

Realizar os testes com uma maior quantidade e maior variedade de sinais: Nos testes implementados até aqui utilizei apenas 3 sinais de voz, sintetizando apenas a vogal /a/. Para uma melhor análise dos resultados, vai ser importante testar o método com vários sinais, havendo entre eles a síntese de todas as vogais.
Implementar outros métodos e comparar: Utilizando os mesmo sinais utilizados para o teste do método proposto³, pretendo implementar e testar o método proposto por Alku et al. [bibcite key=alku2013formant] e outros métodos de outros trabalhos para uma comparação mais adequada e completa com os resultados obtidos pelo método aqui apresentado.

Além desses dois pontos que receberão um maior foco daqui pra frente, também creio que seja válido retornar ao classificador que implementei no TCC⁴, utilizando o novo método para a estimação de formantes e verificar a influência da mudança nos resultados. Porém, como havia pretendido anteriormente, farei uma pausa por agora e somente mais pra frente voltarei a fazer relatórios.

Hum, sei… Mas e quais foram mesmo as referências?

[/bibshow]

Sobre o Autor

Jônatas Cruz Santos

jonatascrs@live.com | CV Lattes

Mestrando em Engenharia Elétrica e Bacharel em Engenharia Eletrônica pela Universidade Federal de Sergipe. Interessado nas áreas de Modelagem Computacional, Processamento Digital de Sinais, Processamento Digital da Fala e Reconhecimento de Padrões. Atualmente desenvolve pesquisa no estudo de modelos computacionais dos mecanismos de produção vocal.

Áreas de Pesquisa: Modelagem Computacional, Processamento Digital de Sinais, Reconhecimento de Padrões, Processamento de Sinais de Voz e Fala, Qualidade Vocal.

Para não me estender muito, não revisarei a predição linear, que já foi bastante explicada e reexplicada em vários relatórios do grupo (em caso de dúvidas, consulte o médico e leia o relatório anterior).
Mesóclises são maravilhosas. Usá-las-ei com certeza!
Se ele for realmente útil, vai precisar de um nome.
Classificador de Qualidade Vocal em Escalas de Avaliação Perceptivo-Auditiva.

Biochaves

Estimação de Formantes por Preditor Linear de Ordem Variável – Removendo a Influência da f0

Ué, mas você não disse que ia fazer uma pausa nos relatórios? O que foi feito dessa vez?

Sim, aquele método! Bem… como ele era mesmo?

Os sinais sintetizados

As medidas para avaliar o método

O resultado anterior

Ah, lembrei! Mas e agora?

Estimação de frequência fundamental por autocorrelação

Filtragem Inversa

Ok então, estou calmo. Como você usou isso tudo pra melhorar o resultado?

Caramba, melhorou bastante mesmo! E agora, quais os próximos passos?

Hum, sei… Mas e quais foram mesmo as referências?

Jônatas Cruz Santos

Deixe uma resposta Cancelar resposta

Posts recentes

Categorias

Se inscreva na nossa Newsletter!