Mais sobre (chocolates de Dalí e) deformação de sinais de fala…

No post:

http://biochaves.website/manual-tao-simples-quanto-possivel-para-deformacao-temporal-e-frequencial-de-sinais-de-fala/

a edição de sinais de fala foi abordada através da manipulação direta de segmentos de sinais. Essa abordagem tem o mérito de ser muito simples e intuitiva. Neste post, contudo, usaremos a teoria de predição linear, já apresentada no post

http://biochaves.website/introducao-a-predicao-linear-com-aplicacao-em-sinais-de-voz/

como uma via mais elaborada para a deformação temporal e de frequência fundamental de sinais de fala.

Assim como no post anterior, será usado o Scilab como plataforma para ilustrar o princípio. Para começar, o arquivo chocolate0.wav será usado na ilustração, e o primeiro passo deve ser a importação do sinal (das sua amostras) para o ambiente onde o processamento será feito. No Scilab, isso deve ser feito com o seguinte comando:

[s,fa]=wavread('chocolate0.wav'); // Este arquivo pode ser obtido no link abaixo

Link para o arquivo:

onde s é o vetor de 18000 amostras colhidas a uma taxa fa=22050 amostras/segundo.

sound(s,fa);   // Este comando envia o vetor de amostras (ou sinal digital) s para a placa de som do computador, onde um conversor Digital/Analógico recupera o som, na taxa de amostragem fa.

 

podemos ver o sinal inteiro num gráfico (plano cartesiano) em que o eixo horizontal é o tempo discreto (contador de amostras), e o eixo vertical corresponde à escala de valores das amostras (proporcionais à pressão do ar ao longo do tempo, como captado pelo microfone).

plot(s)

 

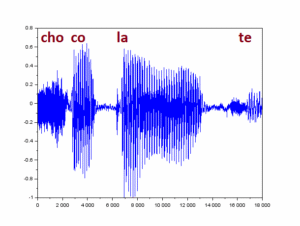
O primeiro passo de processamento corresponde a um filtro passa-altas que, além de reforçar os harmônicos, leva o nível médio do sinal a perto de zero.

s=s(2:$)-0.95*s(1:$-1);

Em seguida, como se deseja analisar o sinal apenas uma vez a cada 10 ms, considerando apenas uma janela de 30 ms (pois é assumido que o sinal de fala se mantém estacionário num intervalo assim tão curto), são definidas duas variáveis:

Janela=round(0.03*fa); // Número de amostras correspondentes a 30 ms de sinal

Avanco=round(0.01*fa); // Número de amostras correspondentes a 10 ms de sinal

Outra escolha importante é a ordem preditor, que deve ser ainda mais curta (muito mais curta) que a janela de observação:

Ordem=round(0.001*fa); // Número de amostras correspondentes a 1 ms de sinal

A deformação do sinal pode ser organizada em duas etapas: a de análise e a de ressíntese.

Etapa de análise do sinal

Na etapa de análise, um preditor linear da ordem escolhida acima é ajustado para cada janela de 30 ms, e os coeficientes dos muitos preditores obtidos ao longo do tempo são guardados na matriz CP, onde cada coluna corresponde a uma janela temporal de sinal analisado. Portanto, convém inicializar essa matriz como vazia antes do início da etapa de análise:

CP=[];

Também em cada janela de 30 ms de sinal, são analisadas e guardadas a potência do sinal e a taxa de cruzamentos por zeros dos segmentos de sinal encontrados nesses intervalos. As medidas de potência do sinal e taxa de cruzamentos por zeros  são guardadas nos vetores Pot e TCZ, que também são inicializados como vetores vazios:

Pot=[];

TCZ=[];

Agora o laço de análise do sinal pode ser executado, como no código comentado abaixo:

for k=1:Avanco:(length(s)-Janela) // a variável de controle k avança a passos iguais a 'Avanco' amostras até o final do sinal, com um recuo de 'Janela' amostras por garantia.

    saux=s(k:k+Janela-1); // um segmento do sinal s de tamanho 'Janela' amostras (correspondente a 30 ms) é tomado para análise

    // Computação da potência do segmento de sinal:

    Pot=[Pot mean(saux.^2)]; // A potência do segmento de sinal saux é anexada ao vetor de potências.

    // Computação da taxa de cruzamento por zeros do segmento de sinal:

    pz=find(saux(2:$)>0 & saux(1:$-1)<0); //pz corresponde aos instantes de cruzamento por zero no sentido ascendente

    TCZ=[TCZ length(pz)*fa/Janela];

    // Computação dos coeficientes de predição linear do segmento de sinal:

    S=[];

    for m=1:Ordem+1,
        // 'Ordem' segmentos de aproximadamente 30 ms de sinal são organizados nas colunas da matriz S. 
        // Cada coluna corresponde a uma versão do mesmo sinal deslocado (atrasado) em uma amostra (1/fa segundos).
        S=[S saux(m:$-(Ordem+1)+m)']; 
    end

    C=pinv(S(:,1:$-1))*S(:,$); // Usando a pseudo-inversão, é possível se estimar um conjunto de coeficientes C que, quando usados como pesos na soma ponderada das primeiras colunas de S, geram com mínimo erro (quadrático) de reconstrução a última coluna de S. Ou seja, C corresponde aos coeficientes ótimos do preditor linear, sob o critério do erro quadrático.

    CP=[CP C]; // Cada preditor linear (representado pelo vetor de coeficientes C) deve ocupar uma coluna de CP.

end

Etapa de ressíntese

Como resultado da etapa de análise, dois vetores, Pot e TCZ, e uma matriz, CP, foram obtidos, todos com o mesmo número de colunas. Cada coluna corresponde portanto a uma janela de análise de 30 ms do sinal original, com avanços de 10 ms. Na ressíntese,  podemos alterar:

a) a duração total do sinal, alterando o intervalo de tempo correspondente a cada janela – Por exemplo, se cada coluna das variáveis Pot, TCZ e CP for usada para gerar 15 ms, ao invés dos 30 ms usados na análise, então o sinal ressintetizado terá metade da duração do sinal original;

b) a frequência fundamental associada aos intervalos com sinais periódicos –  Como o preditor linear não codifica o sinal periódico do pulso glotal, mas apenas as ressonâncias do trato vocal, então o sinal pode ser ressintetizado com a periodicidade desejada, e processado pelo filtro digital correspondente ao preditor em cada janela, gerando assim um timbre semelhante ao do sinal original, mas em outra frequência fundamental;

c) É possível também se alterar apenas o timbre do sinal gerado pela manipulação direta dos polos da função de transferência do filtro correspondente ao preditor em cada janela, esse tipo de modificação será tratado no final deste post.

Tanto a modificação/distorção (a) quanto a (b) precisam de dois sinais a serem misturados na ressíntese: um ruidoso, r(n), e outro vocalizado, v(n). A construção de ambos já deve incluir as alterações de tempo e de frequência fundamental, F0. Portanto, começamos o processo de ressíntese definindo perfis de tempo e de F0, assim:

K=length(s); // Comprimento/duração, em amostras, do sinal original.

perfilTempo=0.1+4*([0:K]/K); // Exemplo de perfil de tempo que inicia com 1/10 da velocidade original e termina 4.1 vezes mais rápido (fala lenta -> fala rápida)

apontador=floor(cumsum(perfilTempo)); // Este vetor apontador é responsável pela distorção temporal, relacionando tempos no sinal original a tempos distorcidos no sinal ressintetizado

N=apontador($);  // Comprimento/duração, em amostras, do sinal ressintetizado.

perfilF0=80-30*([0:N]/N); // Exemplo de perfil de F0 que inicia com 80 Hz e termina com apenas 50 Hz (fala grave -> fala ainda mais grave)

r=rand(1,N,'normal');  // Fonte de sinal ruidoso com potência unitária (desvio padrão igual a 1)

// Construção do sinal vocalizado de acordo com o perfil de  F0:

v=zeros(1,N);

pp=round(fa/perfilF0(1)); // pp deve apontar a posição onde o próximo pulso glotal deve aparecer, de acordo com o F0 instantâneo

v(pp)=1;

while pp<N

    pp=pp+round(fa/perfilF0(pp));

    v(pp)=1;

end

// Agora que o sinal v(n) contém um trem de impulsos devidamente posicionados, respeitando o perfil de F0, é preciso gerar um pulso glotal artificial, como segue:

N1=fa*0.001;

N2=fa*0.0005;

g=[0.5*(1-cos(%pi*[0:N1]/N1)) cos(%pi*[0:N2]/(2*N2))]; // Pulso de Rosenberg

// Rosenberg, A.E., 1971. Effect of glottal pulse shape on the quality of natural vowels. The Journal of the Acoustical Society of America, 49(2B), pp.583-590.

v=convol(g,v); // Esta convolução trata de colocar um pulso glotal em cada posição marcada com um impulso em v(n);

v=v/stdev(v); // Finalmente, o sinal vocalizado tem sua potência normalizada, assim como o sinal de ruído r(n).

Como última etapa, o sinal ressintetizado pode finalmente ser reconstruído no vetor y(n), como explicado a seguir:

y=zeros(1,N);

[ordem,ncol]=size(CP);

passo=floor(K/ncol);

n_ini=ordem+1;

for col=1:ncol

    if TCZ(col)<2000 // Aqui é decidido se o sinal é vozeado (TCZ<2000) ou não. Assim, a composição da fonte pode ser 90 % vozeada e 10 % ruidosa, ou o contrário.

        vozeado=0.9;

    else

        vozeado=0.1;

    end

    ganho=sqrt(Pot(col)); // O ganho de amplitude associada a cada instante de tempo é proporcional à raiz quadrada da potência instantânea
    n_fim=apontador(passo*col);

    for n=n_ini:n_fim

        // Neste laço interno, cada amostra do sinal ressintetizado y(n) é construída a partir do modelo linear do trato vocal variante no tempo, representado pelos coeficientes de predição, e de uma excitação modelada pela combinação linear de um ruído e de um sinal vocálico com pulsos glotais sintéticos, cujo ganho também é controlado pelo perfil de potência do sinal analisado.

        y(n)=y(n-1:-1:n-ordem)*CP($:-1:1,col)+ganho*(vozeado*v(n)+(1-vozeado)*r(n));

    end

    n_ini=n_fim;

end

y=y/max(abs(y));

sound(y,fa);

Para os parâmetros perfilTempo e perfilF0 escolhidos na ilustração acima, o resultado soa como um ‘agravamento’ da voz original (cujo F0 original se encontra no entorno de 120 Hz – voz masculina média) e numa distorção no ritmo da fala que pode ser escutada com a execução do código, ou no ‘play’ abaixo:

Para facilitar a comparação, o ‘play’ do sinal original foi copiado aqui:

 

Outras alterações podem ser obtidas apenas com a redefinição dos parâmetros  perfilTempo e perfilF0, como por exemplos:

perfilTempo=2-0.5*([0:K]/K);
perfilF0=200+50*([0:N]/N);

perfilTempo=1-0.8*cos(%pi*[0:K]/K); 
perfilF0=[120*ones(1,N/3) 250*ones(1,N/3) 300*ones(1,N/3)]; // Atenção ao salto de F0: de 120 Hz para 250 Hz, depois para 300 Hz.

perfilTempo=0.5+0.2*([0:K]/K);
perfilF0=250+50*([0:N]/N);

perfilTempo=3.5+0.5*([0:K]/K);
perfilF0=250+50*([0:N]/N);

 

Por conveniência daqueles que queiram ‘copiar-colar’ o código na plataforma Scilab, ei-lo 🙂

// Leitura e filtragem do sinal:
[s,fa]=wavread('chocolate0.wav');
s=s(2:$)-0.95*s(1:$-1);


// Análise:
Janela=round(0.03*fa);
Avanco=round(0.01*fa);
Ordem=round(0.001*fa);
CP=[];
Pot=[];
TCZ=[];
for k=1:Avanco:(length(s)-Janela) 
    saux=s(k:k+Janela-1); 
    Pot=[Pot mean(saux.^2)];  
    pz=find(saux(2:$)>0 & saux(1:$-1)<0); 
    TCZ=[TCZ length(pz)*fa/Janela];
    S=[];
    for m=1:Ordem+1,
        S=[S saux(m:$-(Ordem+1)+m)'];
    end
    C=pinv(S(:,1:$-1))*S(:,$); 
    CP=[CP C];
end


// Ressíntese
K=length(s);
perfilTempo=0.1+4*([0:K]/K);
apontador=floor(cumsum(perfilTempo));
N=apontador($);
perfilF0=80-30*([0:N]/N);
r=rand(1,N,'normal');
v=zeros(1,N);
pp=round(fa/perfilF0(1));
v(pp)=1;
while pp<N
    pp=pp+round(fa/perfilF0(pp));
    v(pp)=1;
end
N1=fa*0.001;
N2=fa*0.0005;
g=[0.5*(1-cos(%pi*[0:N1]/N1)) cos(%pi*[0:N2]/(2*N2))];
v=convol(g,v);
v=v/stdev(v);
y=zeros(1,N);
[ordem,ncol]=size(CP);
passo=floor(K/ncol);
n_ini=ordem+1;
for col=1:ncol
    if TCZ(col)<2000
        vozeado=0.9;
    else
        vozeado=0.1;
    end
    ganho=sqrt(Pot(col));
    n_fim=apontador(passo*col);
    for n=n_ini:n_fim
        y(n)=y(n-1:-1:n-ordem)*CP($:-1:1,col)+ganho*(vozeado*v(n)+(1-vozeado)*r(n));
    end
    n_ini=n_fim;
end
y=y/max(abs(y));
sound(y,fa);

 

Alteração do timbre do sinal gerado

A análise através da predição linear tem o mérito de modelar as ressonâncias do tubo (de músculos, cartilagens, dentes e mucosa) que transformam o som que vem da garganta em voz como conhecemos e escutamos normalmente. Isto é, cada coluna da matriz CP contém coeficientes de um filtro digital que representa o próprio trato vocal, numa janela temporal curta o suficiente para que o formato do trato possa ser aproximado como estacionário (por isso usamos um parâmetro ‘Janela’ correspondente a poucas dezenas de milisegundos).

A teoria de sistemas lineares nos ensina que as ressonâncias de uma estrutura correspondem a polos da função de transferência que representa essa estrutura. No caso da garganta, esses polos correspondem ao tamanho/volume interno da garganta. Por isso, um homem que tenta imitar a voz de uma mulher apenas alterando a frequência fundamental de sua voz soa artificial, isto é, não soa como uma verdadeira voz feminina, mesmo que o F0 esteja na faixa de valores esperada para uma mulher.

Para que a voz masculina soe feminina de maneira mais convincente, é preciso alterar o ‘volume interno’ do trato vocal, e isso corresponde a alterar as frequências naturais de ressonância da cavidade, que são as frequências associadas aos polos mais importantes da função de transferência que modela o trato vocal. Em geral, essas ressonâncias estão entre 100 Hz e 3000 Hz, e elas podem variar para cima, para provocar o efeito de redução do volume das cavidades do trato vocal  (voz masculina -> voz feminina), ou para baixo, caso contrário  (voz feminina -> voz masculina). Essas variações ocorrem numa proporção de aproximadamente 20 % das frequências de ressonância. Por exemplo, ressonâncias no entorno de 500 Hz podem subir ou descer aproximadamente 100 Hz, enquanto as ressonâncias no entorno de 3000 Hz podem subir ou descer aproximadamente 600 Hz. Essas aproximações são grosseiras, e embora sirvam a esta ilustração de princípios, pode ser trabalhada com mais cuidado para gerar efeitos mais realistas.

Para realizar essa transformação de timbre correspondente à modificação das ressonâncias de forma mais conveniente, é definida abaixo uma ‘função’ que modifica os coeficientes de predição em cada coluna de CP de acordo com a variação proporcional de frequência dada pela variável ‘fator’. Por exemplo, se fator=0.2, então as ressonâncias entre 100 Hz e 3000 Hz serão alteradas para cima em 20%, ficando com um timbre mais feminino. Por outro lado, um fator de -0.2 abaixará as ressonâncias em 20%, dando a impressão de uma estrutura ressonante (um trato vocal) mais volumoso, como os masculinos.

function [NCP]=modifSpec(CP, fator, fa)

cosAngMin=cos(100*2*%pi/fa); // O menor ângulo a ser modificado corresponde a 100 Hz

cosAngMax=cos(3000*2*%pi/fa); // O maior ângulo a ser modificado corresponde a 3000 Hz


[ordem,ncol]=size(CP);

NCP=zeros(ordem,ncol);

for col=1:ncol

    C=CP(:,col);

    H=poly([-C; 1],'z','coeff');

    R=roots(H);

    

    ro=abs(R);

    

    // Alteração de formantes entre 100 Hz e 3000 Hz

    a=real(R);

    b=imag(R);

    deltaW=fator*atan(b./a);

    

    posPolosSup=find(b>0 & ro>0.9 & a<=cosAngMin & a>=cosAngMax);

    posPolosInf=find(b<0 & ro>0.9 & a<=cosAngMin & a>=cosAngMax);

    

    NR=R;

    NR(posPolosSup)=(a(posPolosSup).*cos(deltaW(posPolosSup))-b(posPolosSup).*sin(deltaW(posPolosSup)))+%i*(b(posPolosSup).*cos(deltaW(posPolosSup))+a(posPolosSup).*sin(deltaW(posPolosSup)));

    NR(posPolosInf)=(a(posPolosInf).*cos(deltaW(posPolosSup))+b(posPolosInf).*sin(deltaW(posPolosSup)))+%i*(b(posPolosInf).*cos(deltaW(posPolosSup))-a(posPolosInf).*sin(deltaW(posPolosSup)));

    aux=real(coeff(poly(NR,'z','roots')))';

    NCP(:,col)=-aux(1:$-1);

end

endfunction

Para experimentar o efeito dessas transformações de forma destacada, podemos ressintetizar o sinal com perfil de F0 e de tempo constantes, alterando apenas as ressonâncias, ora para cima (fator=0.2), ora para baixo (fator=-0.2). O código para a ressíntese é dado abaixo:

// Comente uma das duas linhas abaixo para obter os efeitos de diminuir ou aumentar o volume do trato vocal:

fator=0.2; // Para cima

//fator=-0.2; // Para baixo


[NCP]=modifSpec(CP,fator,fa);

// Ressíntese
K=length(s); // Comprimento/duração, em amostras, do sinal original.
perfilTempo=ones(1,K);
apontador=floor(cumsum(perfilTempo)); // Este vetor apontador é responsável pela distorção temporal, relacionando tempos no sinal original a tempos distorcidos no sinal ressintetizado
N=apontador($); // Comprimento/duração, em amostras, do sinal ressintetizado. 
perfilF0=120*ones(1,N); 
r=rand(1,N,'normal'); // Fonte de sinal ruidoso com potência unitária (desvio padrão igual a 1)
// Construção do sinal vocalizado de acordo com o perfil de  F0:
v=zeros(1,N);
pp=round(fa/perfilF0(1)); // pp deve apontar a posição onde o próximo pulso glotal deve aparecer, de acordo com o F0 instantâneo
v(pp)=1;
while pp<N
    pp=pp+round(fa/perfilF0(pp));
    v(pp)=1;
end
// Agora que o sinal v(n) contém um trem de impulsos devidamente posicionados, respeitando o perfil de F0, é preciso gerar um pulso glotal artificial, como segue:
N1=fa*0.001;
N2=fa*0.0005;
g=[0.5*(1-cos(%pi*[0:N1]/N1)) cos(%pi*[0:N2]/(2*N2))]; // Pulso de Rosenberg
v=convol(g,v); // Esta convolução trata de colocar um pulso glotal em cada posição marcada com um impulso em v(n);
v=v/stdev(v); // Finalmente, o sinal vocalizado tem sua potência normalizada, assim como o sinal de ruído r(n).
y=zeros(1,N);
[ordem,ncol]=size(NCP);
passo=floor(K/ncol);
n_ini=ordem+1;
for col=1:ncol
    if TCZ(col)<2000
        vozeado=0.9;
    else
        vozeado=0.1;
    end
    ganho=sqrt(Pot(col));
    n_fim=apontador(passo*col);
    for n=n_ini:n_fim
        y(n)=y(n-1:-1:n-ordem)*NCP($:-1:1,col)+ganho*(vozeado*v(n)+(1-vozeado)*r(n));
    end
    n_ini=n_fim;
end
y=y/max(abs(y));
sound(y,fa);

O resultado desse terceiro tipo de modificação de fala pode ser percebido nos seguintes áudios (a notar que os perfis de F0 e de tempo são absolutamente iguais) :

Sem efeito (fator=0):

Trato vocal com volume aumentado em 20 % (fator=+0.2):

Trato vocal com volume reduzido em 20 % (fator=-0.2):