Introdução

Olá, boa noite. Meu nome é Luiz Miranda e hoje irei falar sobre Análise de Sistemas Lineares. Mais precisamente, análise de Sinais.

Antes de começar, eu me pergunto, ou melhor, pergunto a vocês, o que é um sinal?

De tudo que vocês já ouviram falar na vida, acho que podemos dizer que as ondas eletromagnéticas que transmitem a TV, rádio e Internet podem ser chamadas de sinais, certo? Isso mesmo, outro exemplo que podemos dar de sinal é a voz, ou melhor, o som. A variação de pressão transmitida pelo ar que sai da minha boca e chega aos seus ouvidos também pode ser considerada um sinal. Uma imagem também pode ser considerada uma sinal, ou não? Intuitivamente, alguns de vocês dirão que sim. Mas o que é que todos esses supostos sinais têm em comum? O que o sinal de TV e rádio estão transmitindo? O que podemos extrair de uma imagem? Se você pensou informação você está no caminho certo.

O livro Sinais e Sistemas Lineares, do B. P. Lathi, define sinal como um conjunto de dados ou informação. Já C. E. Shannon, no seu revolucionário artigo A Mathematical Theory of Communication, coloca o sinal como o portador da mensagem que deve ser transmitida, no esquema visto na Figura 1.

Figura 1. Esquema geral de um sistema de comunicações. [Shannon]

No final das contas, podemos dizer que sinal é algo de que podemos extrair informação. Essa definição é um tanto quanto generalista demais, por que podemos extrair informação de praticamente qualquer coisa. Para simplificar nossas vidas, iremos estudar sinais que variam apenas em função do tempo. Como assim? Quem pode me dar um exemplo de um sinal que varia apenas com o tempo? A quantidade de luz que uma planta recebe durante o dia é um sinal variante no tempo. O valor de tensão em um sensor durante um período, também. Então, para nós, matematicamente, qualquer função x(t) pode ser chamada de sinal.

Nosso sinal, ou função x(t), possui duas informações essenciais que são: Energia e Potência. Ambas são uma medida do tamanho do sinal. Vamos dar uma olhada nelas.

Energia do Sinal

Um sinal, como já falamos é uma função x(t). Para sabermos quais tipos de sistemas devemos usar para gerar, ou processar, esses sinais, precisamos saber o tamanho dele. Tamanho? Como assim? Considere o sinal g(t) abaixo.

Como podemos medir o tamanho? Uma forma que pode parecer clara é medir o quanto o sinal varia em amplitude durante um certo período de tempo, certo? Neste caso, o sinal varia 5 unidades no instante 1s e varia novamente 5 unidades no instante 2s. Como colocar um valor nesse tamanho agora? Podemos dizer que é o produto da variação de amplitude pela variação de tempo. Ou seja, 5 vezes 1. E temos aí uma medida de tamanho. Mas se esse sinal tivesse um pedaço negativo, como no sinal h(t) abaixo?

Parece que teríamos a mesma coisa, não é? Para medir o tamanho deste sinal, calcularíamos a área sobre h(t), certo? O problema é que a área sobre h(t) é zero. Consegue ver isso? Então, como resolver este problema? Que tal encontrarmos a área sobre o sinal ao quadrado? Assim evitamos que partes negativas ocorram e o formato geral do sinal meio que se mantém. Fazendo isso para g(t) temos que seu tamanho é 25×1 e para h(t) temos que seu tamanho também é 25×1. O que isso significa? Os sinais são diferentes mas têm a mesma energia? Isso mesmo, essa medida não é uma identidade do sinal e sim uma medida de quanta energia pode ser extraída do sinal, ou quanta energia é necessária para gerar o sinal. Opa, falamos em energia, não foi? E é justamente isso que usamos para calcular a energia do sinal, a área do sinal ao quadrado. Formalizando isso matematicamente para qualquer sinal x(t) temos que:

$E_x = \int_{-\infty}^{\infty}{x^2(t) dt}$

Potência do Sinal

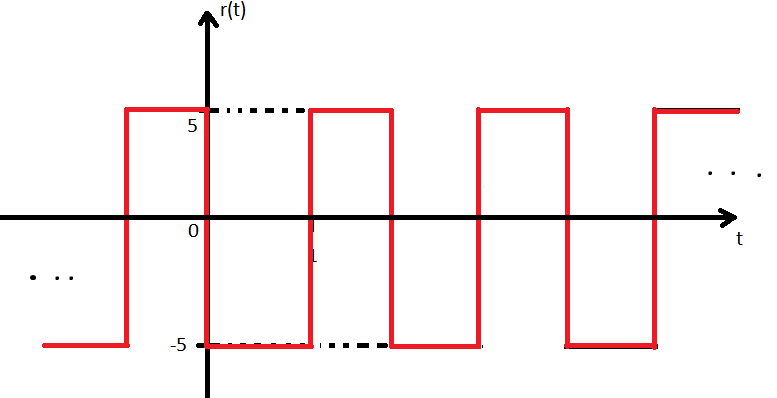
Agora que sabemos uma forma de medir tamanho de sinais vamos ver mais uma. Mas antes vamos tentar calcular o tamanho do sinal r(t) abaixo usando as ferramentas que já conhecemos.

Eita, o sinal não tem fim. Então o tamanho (energia) dele é infinito. De que me importa a informação que o sinal tem energia infinita? Eu preciso de energia infinita para gerar um sinal infinito? Sim. Essa informação é meio óbvia, portanto não é tão útil para nós. O que poderíamos usar aqui, para medir o tamanho do sinal é a energia média, ou seja, a energia que o sinal gerar (ou consome) em um certo período de tempo dividido por esse valor, vamos usar um ciclo do sinal para isso. Este é o mesmo sinal h(t) que usamos só que repetido várias vezes. Então temos que, um ciclo desse sinal dura 1s. A energia desse sinal em um ciclo é 25 (já fizemos esse cálculo), a energia média então será 25/1, também 25. Formalizando matematicamente temos que, para encontrar a energia média devemos usar o teorema do valor médio do cálculo que diz que:

$f_m = \frac{1}{b-a}\int_{a}^{b}{f(t) dt}$

sendo: fm o valor médio de f(t). Podemos substituir os intervalos de integração por uma variável T (que pode ser interpretada como período do sinal) sem perda de generalidade, ficando assim que:

$f_m = \frac{1}{T}\int_{-T/2}^{T/2}{f(t) dt}$

Queremos calcular o valor médio da energia, então:

$f(t) = E_x = E_x = \int_{-\infty}^{\infty}{x^2(t) dt}$

Então, a energia média será calculada por:

$E_{xm} = \lim_{T\to\infty}\frac{1}{T}\int_{-T/2}^{T/2}{f(t) dt} = P_x$

A energia média de um sinal pode ser, e será, chamada de Potência do sinal (Px). Este valor, é a média temporal do quadrado da amplitude do sinal, ou seja, seu valor médio quadrático. Se tirarmos a raiz quadrada de Px teremos o famoso valor RMS (Root Mean Square) do sinal x(t).

Recapitulando

Como vimos, sinais que são “finitos” têm o seu “tamanho” medido através da sua Energia, são esses chamados de Sinais de Energia. E sinais que são “infinitos” têm seu “tamanho” medido através da sua Potência, são esses os chamados Sinais de Potência.

Sobre o Autor

Luiz Miranda Cavalcante Neto

Possui graduação em Engenharia Elétrica com habilitação em Eletrônica pela Universidade Federal de Sergipe (2014) e mestrado em Engenharia Elétrica pela Universidade Federal de Sergipe (2017). Foi professor voluntário da Universidade Federal de Sergipe no período de 2015/1 lecionando a disciplina de Circuitos Digitais. É Professor substituto de Ensino Básico, Técnico, Tecnológico e Superior do Instituto Federal de Sergipe no Campus Lagarto (IFS-Lagarto). Tem experiência na área de Engenharia Elétrica, com ênfase em Robótica e Reconhecimento de Padrões.

Biochaves

Um cursinho de sistemas lineares – Parte 1 – Sinais: O que são? De onde vem? Para onde vão?

Luiz Miranda Cavalcante Neto

Deixe uma resposta Cancelar resposta

Posts recentes

Categorias

Se inscreva na nossa Newsletter!