Olá novamente. Continuo sendo Luiz Miranda e hoje vamos ver um pouco como podemos manipular a cara de um sinal. Para fazer isso iremos realizar algumas operações no tempo, já que como os sinais dependem apenas do tempo esse é o nosso principal recurso.

Operações no Tempo

Como já vimos, os sinais são definidos como funções variantes apenas no tempo. Sabendo disso, vamos ver algumas operações que podemos fazer com os sinais para manipular sua estrutura no tempo. A primeira operação, e talvez a menos intuitiva, é o deslocamento temporal.

Deslocamento temporal

No deslocamento temporal iremos deslocar o sinal no eixo horizontal do seu gráfico. Quando deslocamos para a esquerda, estamos adiantando o sinal. Quando o deslocamos para a direita, estamos atrasando-o. 

Considere a função f(t)=t, seu gráfico pode ser visualizado na Figura 1. Nesta função temos o seguinte comportamento: Quando  t= -1, f(-1)= -1, quando t=0, f(0)=0, quando t=1, f(1)=1 e por aí vai.

Se quisermos adiantar a função em duas unidades de tempo teremos que substituir a variável t por t+2, tendo assim f(t+2)=t+2. O sinal deslocado terá, agora, o seguinte comportamento: quando t= -2, f(-2+2)= -2+2=0, quando t= -1, f(-1+2)= -1+2=1, quando t= 0, f(0+2)= 0+2=2, quando t= 1, f(1+2)= 1+2=3. Na função original, o eixo horizontal era tocado no instante t=0, na função adiantada isso acontece quando t= -2, ou seja, duas unidades de tempo antes. O gráfico resultante pode ser visto na Figura 2.

Já se quisermos atrasar a função em duas unidades de tempo teremos que substituir a variável t por t-2, tendo assim f(t-2)=t-2. A descrição do novo comportamento do sinal é análoga ao comportamento de quando adiantamos ele, fica como exercício para vocês descreverem o comportamento como fizemos no parágrafo anterior. O gráfico resultante pode ser visto na Figura 3.

Em resumo: se temos um sinal f(t), para adiantarmos ele em T unidades usaremos f(t+T) e para atrasarmos o sinal usaremos f(t-T). A próxima operação que veremos é o escalonamento temporal.

Escalonamento Temporal

Esta operação irá acelerar ou retardar a duração do sinal. Para isso, iremos aplicar operações de divisão e multiplicação por uma constante a1 à variável . Considere novamente a função f(t)=t mostrada na Figura 1. Ao multiplicarmos t por uma constante a=2, teremos e o gráfico resultante pode ser visto na Figura 4. Já ao dividirmos t por uma constante a=2, teremos e o gráfico resultante pode ser visto na Figura 5. Como podemos ver nos gráficos, a multiplicação “achata” enquanto a divisão “estica” a função original.

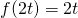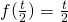Reversão Temporal

Ao aplicarmos essa operação ao sinal ele será espelhado na horizontal. Considere, novamente, o sinal . Aplicar a operação de reversão temporal fará com que a função se torne , ou seja, a variável independente será multiplicada por -1. O resultado disso será que , essa nova função é representada na Figura 6.

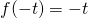Agora que já sabemos as operações no tempo vamos exercitar o uso delas.

Ex:

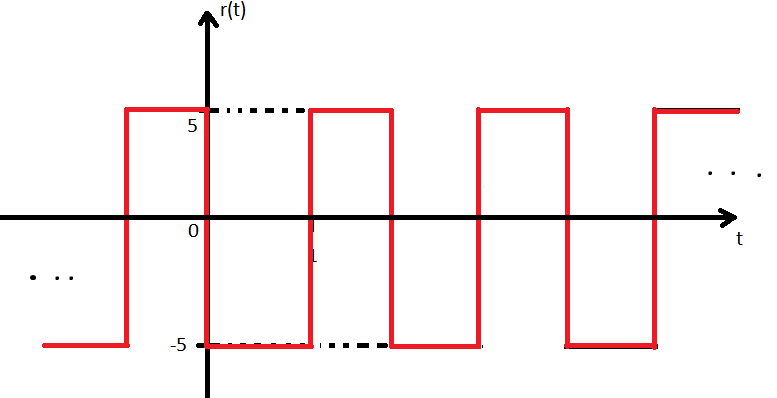
1) Dada a função abaixo esboce:

a)

b)

c)

d)

Sobre o Autor

Luiz Miranda Cavalcante Neto

Possui graduação em Engenharia Elétrica com habilitação em Eletrônica pela Universidade Federal de Sergipe (2014) e mestrado em Engenharia Elétrica pela Universidade Federal de Sergipe (2017). Foi professor voluntário da Universidade Federal de Sergipe no período de 2015/1 lecionando a disciplina de Circuitos Digitais. É Professor substituto de Ensino Básico, Técnico, Tecnológico e Superior do Instituto Federal de Sergipe no Campus Lagarto (IFS-Lagarto). Tem experiência na área de Engenharia Elétrica, com ênfase em Robótica e Reconhecimento de Padrões.

Outras Postagens

• Luiz Miranda Cavalcante Neto

  https://www.biochaves.website/author/luiz-miranda/

  

  23 de março de 2019

  Mapeamento musical de artistas baseado em seus arranjos harmônicos usando cadeias de Markov - Parte 1: O início de tudo
• Luiz Miranda Cavalcante Neto

  https://www.biochaves.website/author/luiz-miranda/

  

  23 de março de 2019

  Mapeamento musical de artistas baseado em seus arranjos harmônicos usando cadeias de Markov - Parte 2: Vendo o mundo com menos dimensões.
• Luiz Miranda Cavalcante Neto

  https://www.biochaves.website/author/luiz-miranda/

  

  23 de março de 2019

  Mapeamento musical de artistas baseado em seus arranjos harmônicos usando cadeias de Markov - Parte 3: Que?!
• Luiz Miranda Cavalcante Neto

  https://www.biochaves.website/author/luiz-miranda/

  

  23 de março de 2019

  Mapeamento musical de artistas baseado em seus arranjos harmônicos usando cadeias de Markov - Parte 4: Aquele das férias.